
Let’s gain an insight into the volume of a cone formula by working out a few example problems.įind the volume of the cone of radius, 5 cm, and height, 10 cm.īy the volume of a cone formula, we have, The slant height, radius, and height of a cone are related as Where V is the volume, r is the radius and h, is the height. The formula for the volume is represented as: The volume of a cone is equal to one-third of the base area’s product and the height. Like all other volumes, the volume of a cone is also expressed in cubic units.

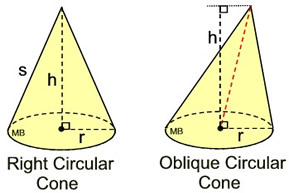
All of these parameters are mentioned in the figure above. A cone’s slanted lines are the length ( L) of a cone along the taper curved surface. In a cone, the perpendicular length between the vertex of a cone and the center of the circular base is known as the height ( h) of a cone.
All cone shapes geometry how to#
In this article, we will discuss how to use the volume of a cone formula to calculate the volume of a cone. In simple words, a cone is a pyramid with a circular base.Ĭommon examples of cones are ice-cream cones, traffic cones, funnels, tipi, castle turrets, temple tops, pencil tips, megaphones, Christmas trees, etc. In geometry, a cone is a 3-dimensional shape with a circular base and a curved surface that tapers from the base to the apex or vertex at the top.


 0 kommentar(er)
0 kommentar(er)
